Why Binary Search?
as you know Napoleon and Hitler both used the Divide-and-Conquer strategy to achieve their goals. This strategy involves dividing their enemies into smaller, more manageable groups and then attacking each group individually. This strategy can be very effective, as it allows the attacker to concentrate their forces on each group and overwhelm them.
Binary Search also Works on Divide and Conquer Approach.
now you might wonder what is Divide and Conquer Approach Let's Deep Dive into it with a Real-life example
imagine you have a big problem that you don't know how to solve. It's like a big puzzle with lots of pieces.
Now, instead of trying to solve the whole puzzle at once, you can break it down into smaller, easier puzzles that you can solve. You can do this by dividing the big puzzle into smaller sections and solving each section one by one.
Then, when you have solved all the smaller puzzles, you can put them back together to get the solution to the big puzzle.
This is what we mean by "divide and conquer" - breaking a big problem down into smaller parts that are easier to solve, and then putting them back together to solve the whole problem.
How Does Binary Search Work? Prerequisites and Explanation.
Let's use a real-life example. Imagine you are looking for a specific book in a library with thousands of books. Instead of searching through all the books one by one, you can use a divide-and-conquer approach. This means you start by checking the middle shelf of the library. If the book is not there, you eliminate half of the library and focus on the other half. You repeat this process by checking the middle shelf of the remaining half until you find the book. This approach is more efficient than searching every single book, and that's why binary search is useful in computer science.
I think Now you have a proper understanding of what Binary Search
For Using Binary Search you must need Sorted Dataset(anything like an array, linked list, a binary search tree, or a sorted matrix), so before using binary search check dataset is sorted or not.
int sortedArray = [1, 3, 4, 6, 7, 9, 11];//It is sorted in Ascending Order
Binary Search Algorithm:)
- Firstly Find the mid element
// Define a sorted array
int[] sortedArray = {1, 3, 4, 6, 7, 9, 11};
// Define the start and end indexes of the array
int start = 0;
int end = sortedArray.length - 1;
// Calculate the mid index by adding the start and end indexes and dividing by 2
int mid = (start + end) / 2;
// However, a more proper way to calculate mid is by subtracting start from half the sum of start and end
int mid = start + (end - start) / 2;
If the middle element is greater than the target element, then we search in the left half of the array.
If the middle element is less than the target element, then we search in the right half of the array.
if the middle element is the target so it is the answer to that.
Code For Binary Search:)
public static int binarySearch(int[] sortedArray, int target) {
int start = 0;
int end = sortedArray.length - 1;
while (start <= end) {
int mid = (start + end) / 2;
if (sortedArray[mid] == target) {
return mid;
} else if (sortedArray[mid] < target) {
start = mid + 1;
} else {
end = mid - 1;
}
}
return -1; // indicates the target was not found
}
Time and Space Complexity
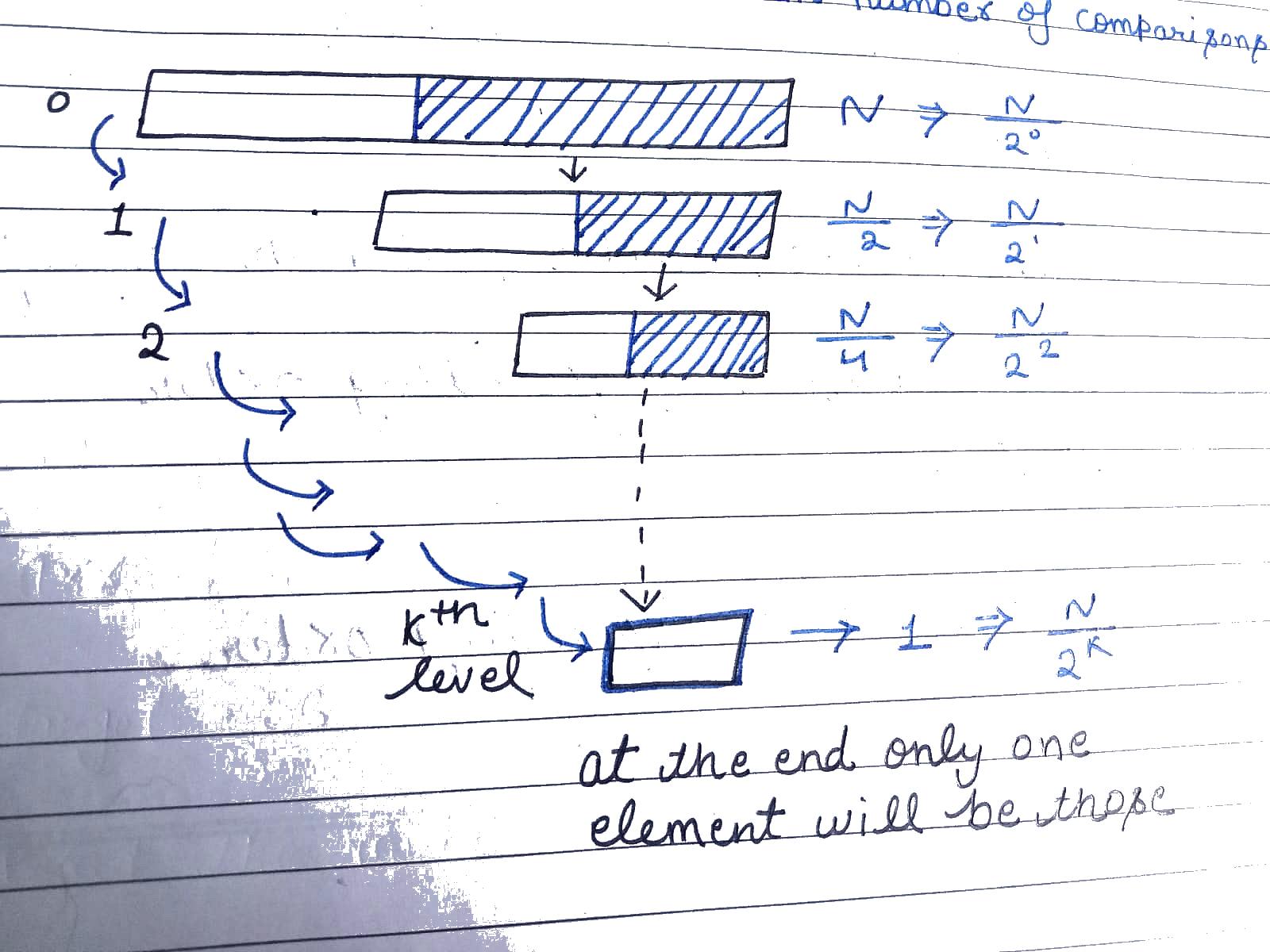
In this you see first we have N elements then N/2 and last 1 which is the kth level

Time Complexity Analysis
In terms of the Best case scenario, the middle of the array provides the most efficient approach, while the worst-case scenario involves the first and last elements of the array, and for average cases, the target element could be located anywhere except the aforementioned cases.
| Best Case | 0(1) | 0(1) |
| Worst Case | O(log n) | O(1) |
| Average case | O(log n) | O(1) |
This is all about the Time Complexity analysis of Binary Search.
Order Agnostic Binary Search
Order agnostic binary search is a variation of the binary search algorithm that can be used to search a sorted array that can be either in ascending or descending order, in previous you saw where we only said data is sorted not mentioning ascending or descending
Algorithm for Order Agnostic binary search
Initialize the start and end pointers of the array.
Check whether the first element of the array is greater than the last element. If yes, then the array is sorted in descending order. Otherwise, the array is sorted in ascending order.
If the array is sorted in ascending order, then use the regular binary search algorithm(Which I tell previously)
If the array is sorted in descending order, then modify the binary search algorithm as follows:
If the middle element is less than the target element, then search in the left half of the array.
If the middle element is greater than the target element, then search in the right half of the array.
If the middle element is equal to the target element, then return the middle index as the answer.
Code For Order Agnostic Binary Search
public static int orderAgnosticBinarySearch(int[] arr, int target) {
int start = 0;
int end = arr.length - 1;
// Determine the order of the array
boolean isAscending = arr[start] < arr[end];
while (start <= end) {
int mid = start + (end - start) / 2;
if (arr[mid] == target) {
return mid;
}
if (isAscending) {
if (arr[mid] < target) {
start = mid + 1;
} else {
end = mid - 1;
}
} else {
if (arr[mid] < target) {
end = mid - 1;
} else {
start = mid + 1;
}
}
}
// Element not found
return -1;
}
In conclusion, binary search is an efficient algorithm for searching sorted datasets by dividing and conquering. It is a fundamental concept in computer science, used in a wide range of applications. Additionally, order-agnostic binary search is a variant that allows for searching datasets in either ascending or descending order, making it a versatile tool. Understanding and applying these techniques can greatly improve the performance of algorithms and programs.
here are some binary search problems on LeetCode that you can try: